数据处理工具-插值计算

工具简介

在对空间数据进行分析时，我们获取的原始数据在空间上往往是不连续的，这是受数据获取方式影响决定的，例如对于城市二手房交易数据，我们只能获取到产生了交易的房产所在点的交易数据，而空间上其他任意点的二手房交易价格往往难以直接获取。使用插值工具可以帮助我们更清晰地了解我们关注的信息在空间中的整体分布状态，预估空间中未知点的信息。

位和平台插值工具能根据已知坐标点的属性值（如：温度、人口、时间等），对给定范围内的其他坐标点进行克里金插值，得到新的指定空间分辨率的点数据。

①选择用于插值的空间文件

选择空间文件：在下拉框下拉选择用于插值计算的空间文件，可以是点文件或面文件。

②选择文件中用于插值的属性值的字段名称

选择插值字段：选择文件中可用于进行插值计算的属性字段的名称，该字段必须为数字型字段，用于插值的属性在空间上应具有连续性。

③为输出文件设置格网边长

插值栅格边长（km）：根据实际需要设定输出文件的格网边长，边长单位为千米。

④设置输出文件名，提交运行

设置输出文件名称：给输出的文件命名，若不设置名称，将自动命名为“工具名称_时间”。

完成设置后，点击“提交运行”启动工具。

运行成功后页面上方将会提示完成计算！数据已上传到“我的数据”，可点击打开数据按钮开始访问数据或到数据页面查看启动。

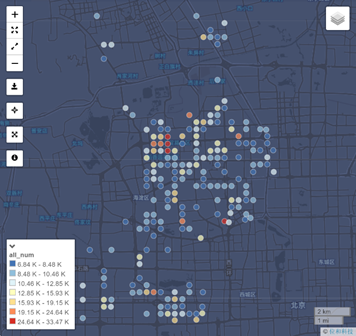
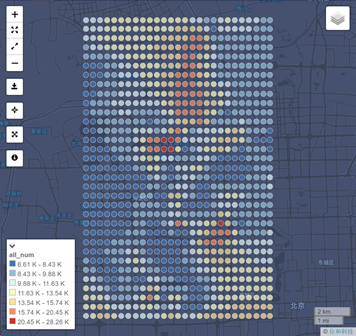
下图为对海淀区人口进行插值前与插值后的图像，插值计算后得到了人口在空间上的连续分布图像，可以更好地反应人口在空间上的变化规律。

克里金插值及高级参数设置

一般在连续的地理空间中，一个空间单元内的信息与其周围单元的信息具有相似性，距离近的单元比距离远的单元更相似，而空间单元的差异常常由三个方面组成，即空间趋势（大尺度结构因素，如从市中心往外围房价逐渐降低）、空间自相关因素（小尺度空间结构因素，如靠近地铁站的房价更高）以及随机误差项。克里金插值模型能根据空间差异的组成，估算出空间中某一点的属性值，这一估计值为对该点周围已知观测值的加权平均值，其本质为一个线性模型，即待估点的值是周围已知观测值的线性组合。

空间中两个点之间距离越远，其属性值差异越大，我们用半变异方差来表征这一差异，半变异方差是相同的距离两个点之间平均的变异程度，半变异方差函数是半变异方差随着两个点之间的距离而变化的函数，随着两点之间距离的增大，半变异方差也随之增大。克里金插值就是利用已有数据拟合半变异函数，建立起空间中点与点之间属性值大小的关系。

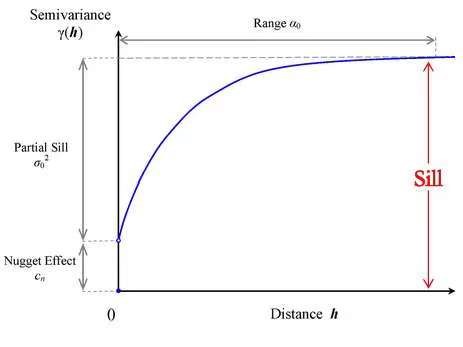
如图为常见半变异方差函数图像，其中包含三个重要参数：块金值（Nugget）、基台值（Sill）和变程（Range）。

块金值：在半变异函数初始端的不连续性所表现的变异性，理论上当两个点距离为0时，半变异方差值应为0，但由于存在空间变异，使得两点距离非常近时，其半变异方差值不为0，即存在块金值。

基台值：又称为最大变异程度，是半变异函数的最大值，而偏基台值（Partial Sill）指的是基台值减去块金值。

变程：存在联系的两点之间最大距离，即半变异方差达到最大值时对应的距离。

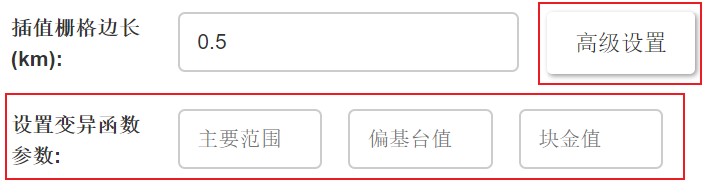
在进行插值计算时，点击“高级设置”按钮，可以对这三个参数进行设置，以得到更为精确的插值效果，但一般不建议自行设置高级设置参数。